Fluctuation Bolometer

K. W. Murch, K. L. Moore, S. Gupta, and D. M. Stamper-Kurn, Measurement of intracavity quantum fluctuations of light using an atomic fluctuation bolometer quant-ph/0706.1005 (June 2007)

In this work we study the properties of temporal intracavity intensity fluctuations in a Fabry-Perot resonator. The most fascinating aspect of these temporal fluctuations is their stark difference from free space, that in a cavity light at the near the frequencies of the cavity resonances is much nosier than light which is in free space, or far from the cavity resonance.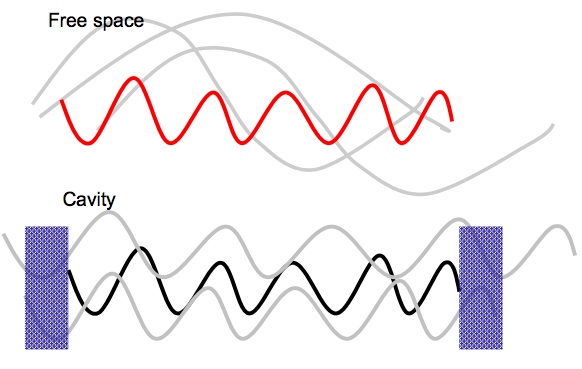

The origin of this effect is as follows; In free space a monochromatic beam is given by a coherent state occupying a specific mode of the electromagnetic field, and vacuum in all the other modes of the electromagnetic field. Temporal fluctuations of this beam result from a beat-note between the coherent state and the electromagnetic vacuum, and since the density of states in free space is flat, the spectrum of these fluctuations is also flat, or white noise.

In a cavity, the density of states of the electromagnetic field is altered by the boundary conditions which the mirrors impose. Here, temporal fluctuations then take on the spectrum of the electromagnetic vacuum, being accentuated near the cavity resonances, and suppressed away from the resonances.

Interestingly, this is a property which can only be detected within the cavity; outside the cavity, the fluctuations remain as in free space. To detect this property of the intracavity field we introduce into the cavity a passive detector of the intracavity fluctuations; far-off resonant atoms. These atoms experience the intracavity intensity as an AC stark shift, and fluctuations of this potential lead to momentum diffusion and heating. For this the diffusion,

{$ 2D = \frac{d}{dt}(\langle p^2\rangle - \langle p \rangle^2) $}

is related to the two-time force correlation,

{$ 2D = \int_0^{\infty} d \tau \cos (\omega_t \tau) \bigl(\langle F(\tau) F(0)\rangle - \langle F(0)\rangle^2 \bigr) $}

Here, forces which fluctuate at {$ \omega_t $} heat the atoms since the atoms are considered to be harmonically confined with trap frequency {$ \omega_t $}. The force {$F$} is given by the gradient of the AC stark shift potential and is proportional to the photon number operator {$\hat{n}$}.

There are, of course other sources of heating for atoms, these `free space' heating rates originate from spontaneous emission of the atom, resulting in recoil kicks, and fluctuations of the dipole force. To accurately sense the fluctuations inside the cavity, we need the cavity induced heating to be larger than the `free space' heating rate, the criterion for this is the condition of single atom strong coupling.

Heating, which may be induced by the aforementioned cavity induced diffusion, by `free space' diffusion, or by technical fluctuations in the probe intensity result in the ejection of atoms from the finite depth optical trap. The equilibrium temperature of the atomic sample results from a balance of the heating rates, and the cooling due to evaporation. A slight increase of this temperature, due to a sudden increase in heating leads to a significant increase in the evaporation rate, returning the temperature to it's equilibrium.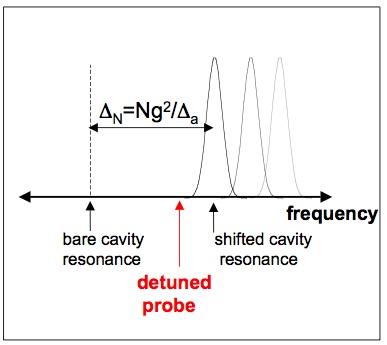

To perform a measurement of the heating rate, we loaded a large number, ~100,000 atoms into the intracavity optical trap. As this number decreased due to a steady background loss rate the shifted cavity resonance frequency decreased. We monitored the transmission of probe light through the cavity as the shifted cavity resonance coincided with the probe frequency. If the atoms were lost from the cavity at a constant rate, we would, in theory, recover the Lorentzian lineshape of the cavity resonance, with the temporal linewidth,

{$\Delta t = \frac{1}{R N}(\frac{\Delta_{a}\kappa}{g^{2}}),$}

indicating the loss rate {$R$}. However, in practice, the heating rate is proportional to the probe intensity, and as the cavity transmission increases, so does the intracavity intensity and the probe light induced heating.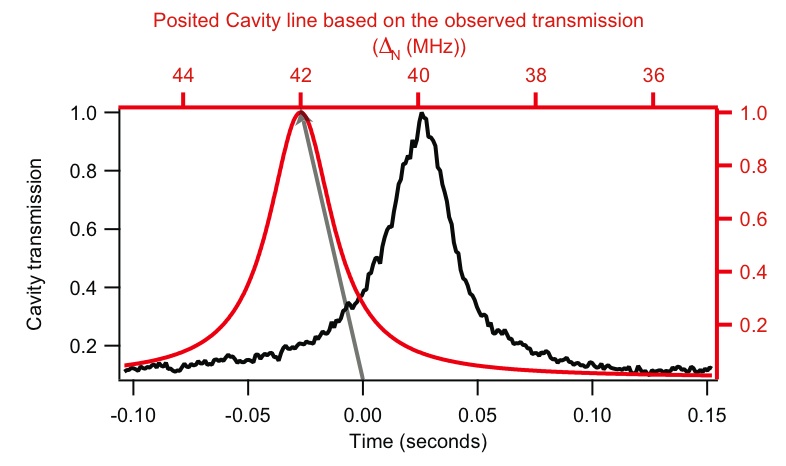

The transmission at each instant is used to infer the probe-cavity detuning {$\delta$} at that moment, given the known cavity lineshape and the magnitude of the cavity drive. There is a slight ambiguity about which side of the cavity resonance is being probed at each instant, which we solve by assuming that the number, and therefore the absolute value of the cavity resonance shift always decreases in time. Given {$\delta$}, we can then obtain the number, and it's rate of change at each instant. We normalize the loss rate to the instantaneous intensity, and given that each lost atom relates to a energy change given by the trap depth, we have a measurement of the heating rate.

Plotted as heating rate versus cavity detuning, the resulting spectrum indicates that the heating is greatly exacerbated near the resonance of the cavity, revealing the cavity induced diffusion.

Away from the cavity resonance, the contribution to the diffusion from the enhanced vacuum fluctuations is negligible, in this case the diffusion should be dominated by the spontaneous emission of the atom, leading to random recoil kicks, and fluctuations of the dipole force. Other sources of light-induced loss, such as technical intensity fluctuations and Raman scattering would also contribute. To demonstrate that the enhanced heating near resonance was clearly resolved, we sought to measure the light induced loss rate away from the cavity resonance. The difficulty of this measurement lies in the the need to apply a controlled `dose' of light, at frequency far from the cavity resonance, and subsequently measure a small fractional loss in number. To accomplish this goal we developed a new set of techniques, here, their use and implementation is presented.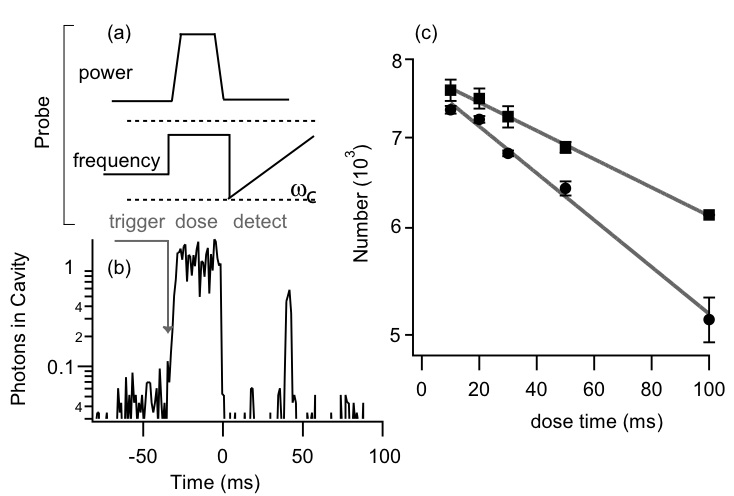

As with the measurement of the resonant heating rate, we begin by loading a large number of atoms into the cavity, and monitoring the transmission of a probe at a fixed frequency. When the transmission of the probe throughout the cavity surpasses a threshold level, we quickly change it's frequency to be detuned from the instantaneous cavity resonance by 30 MHz. Here the intensity of the cavity drive is greatly increased so as to occupy the cavity with ~1 off-resonant intracavity photon. After this dose is applied for a specific period of time, the intensity of the probe is reduced, and the frequency swept between the bare cavity resonance frequency and the initial `trigger' frequency. The resulting spectra is then fit to determine the position of the cavity resonance, and therefore the number.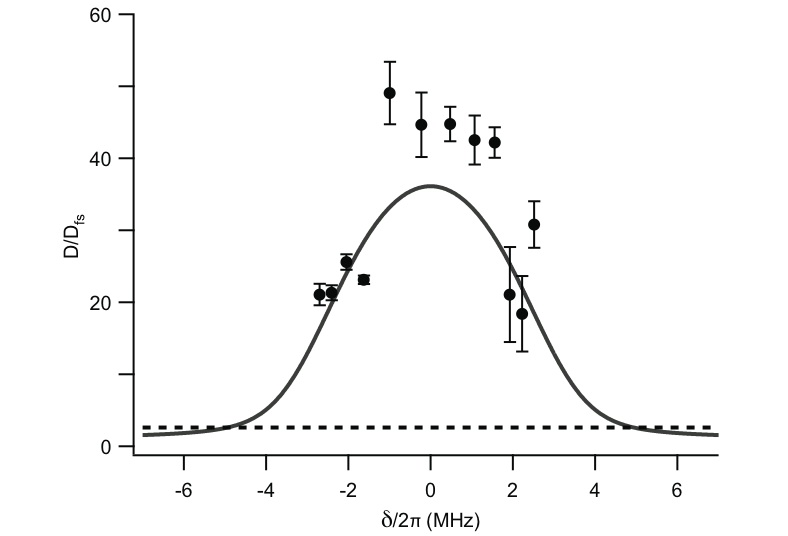

Total Diffusion measured in the Cavity System

The summary of the previously discussed measurements of the total diffusion is shown to the right. Near the resonance, 12 ms sections of transmission data were used to determine the diffusion rate per photon. The dashed line inticates the off-resonant diffusion rate, which we find to be some what larger than the expected free space diffusion. This discrepancy may be explained by additional effects of Raman scattering. Atoms scattered by the {$\sigma^+$} probe light into different hyperfine ground states would couple with different strength to the cavity probe light, thereby changing the relationship between {$\Delta_N$} and the atom number {$N$}. While exothermic hyperfine-changing collisions could lead to trap loss, diminishing {$\Delta_N$} further, the rate of such collisions is expected to be negligibly small for our trapped samples. Given that {$U / (\hbar^2 k^2 / 2 m) = 36$} Rayleigh scattering events are required to eject one atom from the trap, and that Raman scattering occurs {$\simeq 1/8$} as frequently as Rayleigh scattering for our settings, these additional effects appear sufficient to account for our observation. The effects of Raman scattering are constrained by our measurements (dashed line) to contribute only slightly to the atom losses observed from probe light at the cavity resonance.