Research
- E3: cQED, Optomechanics
- E4: Collective modes
of spinor gases - E5: Optical Kagome Lattice
- E6: cQED, Optical lattice Retired Experiments
- E1: Spinor Rubidium BEC
- E2: Cavity QED
Group Information
- People
- Publications
- Theses
- Presentations
- Research Highlights
- Popular Coverage
- Lab news
- Undergraduate research
Links
- January 2016 MURI Review Meeting
- Useful Links
- Review Papers
- Ultracold Coffee Hour
- Bitbucket: AMO@Berkeley
- Our Old Website
- AMO Seminar (PHYS 290F)
Contact InformationLab room: B167 Birge E3: Cavity QED on an Atom Chip Photo of atom chip and cavities By integrating trapped ensembles of ultracold atoms and high-finesse cavities with an atom chip we are able to study and control the classical and quantum interactions between photons and the internal/external degrees of freedom of the atom ensemble. On this page you can find more information on For more details, see Research Highlights.
The Apparatus
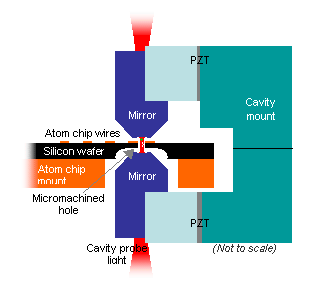 Schematic of an atom chip on a silicon substrate incorporating a Fabry-Perot cavity. A hole is micromachined in the substrate to allow light in the cavity mode to pass through Using copper wires embedded in the atom chip, we magnetically trap and transport an ensemble of ultracold Rb-87 atoms into the optical cavity. We then transfer the ensemble into a single node of a standing-wave, optical dipole trap, resonant with a very far detuned longitudinal mode of the cavity.
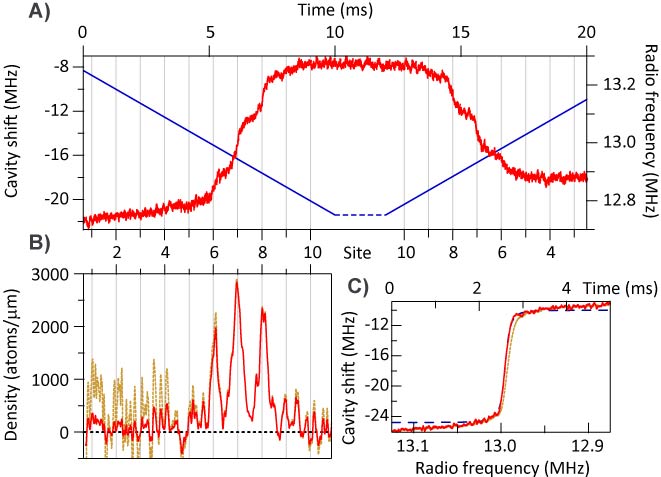
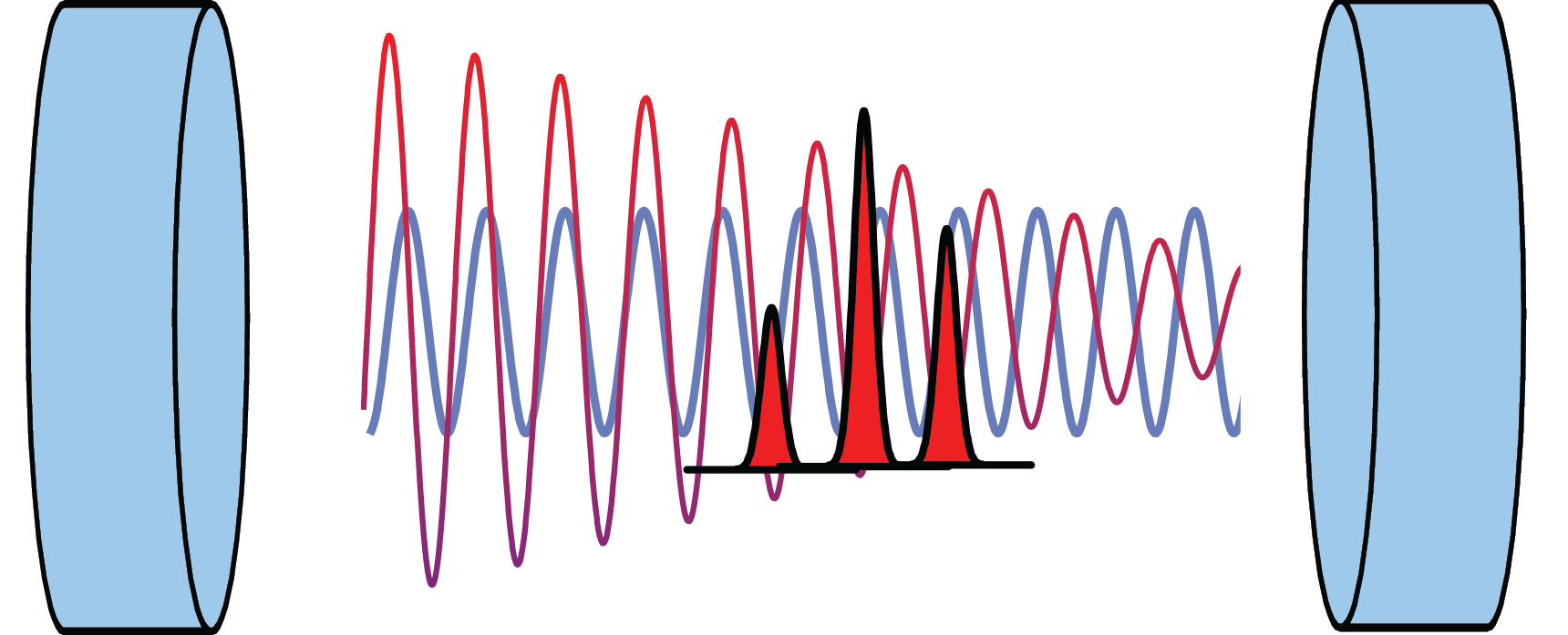
 Cross-Section of chip and cavity. Cavity mirrors are separated by 250 um A 780nm probe laser, resonant with another longitudinal cavity mode, detuned from the atomic D2 transition, dispersively interacts with the atomic ensemble. The coupling of the atomic ensemble to the standing-wave probe intensity is position and spin dependent. Probe light transmitted through the cavity mirrors therefore carries information about the collective position and spin of the ensemble, which is recorded using an optical heterodyne receiver. Spin oscillators in a cavityThe interaction of the probe with the spin of the atomic ensemble results in a scalar and vector Stark shift of the atomic states, along with a dispersive cavity shift proportional to the total atomic spin component along the cavity axis. The vector component of the Stark shift is like an effective magnetic field along the cavity axis, and the dispersive shift facilitates measurement of one component of the total atomic spin. Spin optodynamics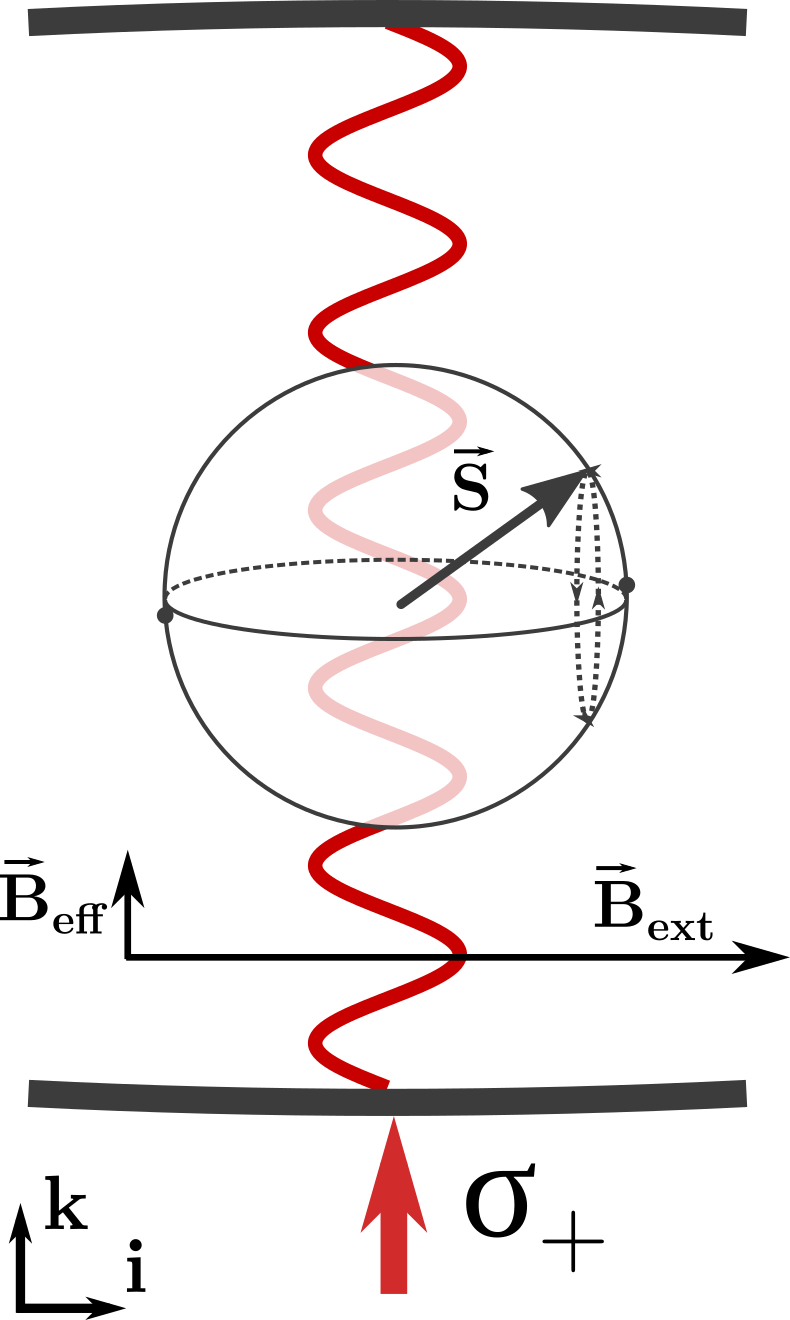 Conceptual diagram of a spin oscillator interacting with the probe laser For small excitations, a spin-polarized atomic ensemble precessing around a transverse magnetic field can be described like a simple harmonic oscillator. The component of the total spin along the cavity axis is measured by the probe, resulting in measurement back-action in the orthogonal component, in order to satisfy the spin uncertainty relation. Considering these the position and momentum of a harmonic oscillator, respectively, this is directly analogous to cavity optomechanics, immediately yielding many similar results as developed in our previous theory paper. Our most recent experimental work has focused on realizing these spin-optodynamics analogues of optomechanics, as well as exploring some of the unique features a spin oscillator presents, such as a widely tunable Larmor frequency, a zero-temperature thermal bath, and a negative temperature, high-energy 'ground state'. Cavity-aided magnetic resonance imagingApplying a large magnetic-field gradient along the cavity axis, we can spatially address spins in different lattice sites using radio-frequency (RF) radiation. By chirping the applied RF, we flip the spins in each lattice site via rapid adiabatic passage. Each flip causes a step in the cavity shift. By taking the derivative of the cavity shift vs. time, we obtain a spatial image of the atom density along the cavity axis.
Tunable optomechanics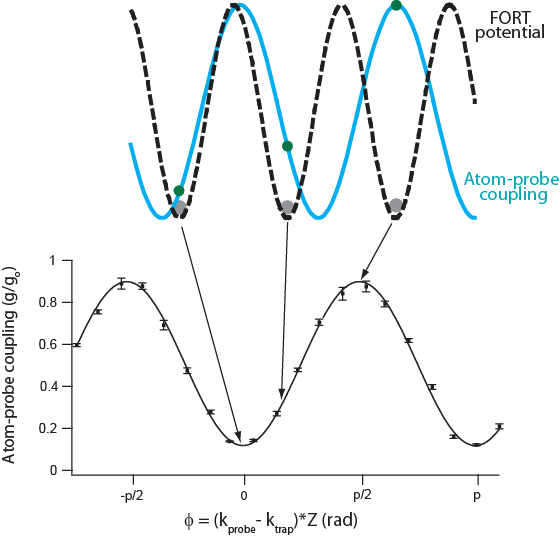 Top Schematic of atom-probe coupling for different well locations. Atoms (grey points) sit at the bottom of the FORT potential (black dashed line). Since the FORT wavelength is incommensurate with that of the probe, different wells lead to different levels of coupling (green dots on blue curve). Bottom Experimentally obtained contrast plot highlighting the atom-probe coupling dependence on the location of the atom cloud. Our experimental setup, based on a micromachined atom chip, allows us to freely position the atoms relative to the probe standing wave. This enables both linear and quadratic optomechanical coupling. The strength of this coupling, along with the mechanical resonator frequency, can be tuned by varying the intracavity probe field intensity and its detuning from atomic resonance. Optomechanical resonators generally consist of solid-state devices. Our atom-based resonator does not suffer from many of the drawbacks found in typical solid-state systems, such as significant environmental couplings, thermal occupation of the mechanical resonator mode, and optomechanical parameters fixed during device fabrication. The ensemble behaves similarly to a dispersive piece of glass, changing the effective length of the cavity. 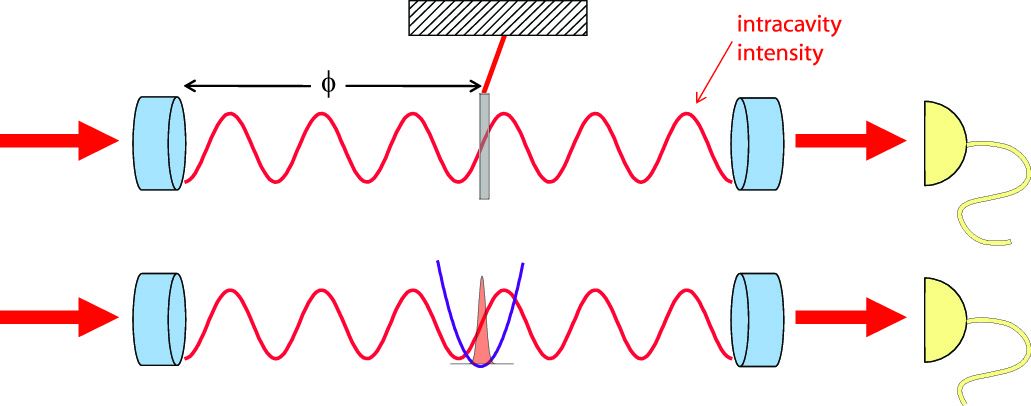 Top Schematic of a piece of glass inside a cavity. Bottom In our experiments, the trapped ensemble provides the phase shift
Optomechanics in a superlatticeWith two optical dipole traps of incommensurate wavelengths, we create an array of loading sites with differing mechanical resonance frequencies, allowing us to separate spectrally the responses of atomic motion from neighboring sites. This mechanical resonance separation technique has allowed us to apply and measure forces with unprecedented sensitivity and to couple mechanical oscillators together via the cavity probe field. For the latter experiment, we can observe the state of each oscillator evolve with or without coupling. Because the photonic coupling field can be measured as it exits the cavity, this kind of coupling necessarily introduces measurement backaction. In order to measure both the coupling-induced energy transfer and the coincident backaction, we acquire a statistical ensemble of many realizations of the coupling measurement.
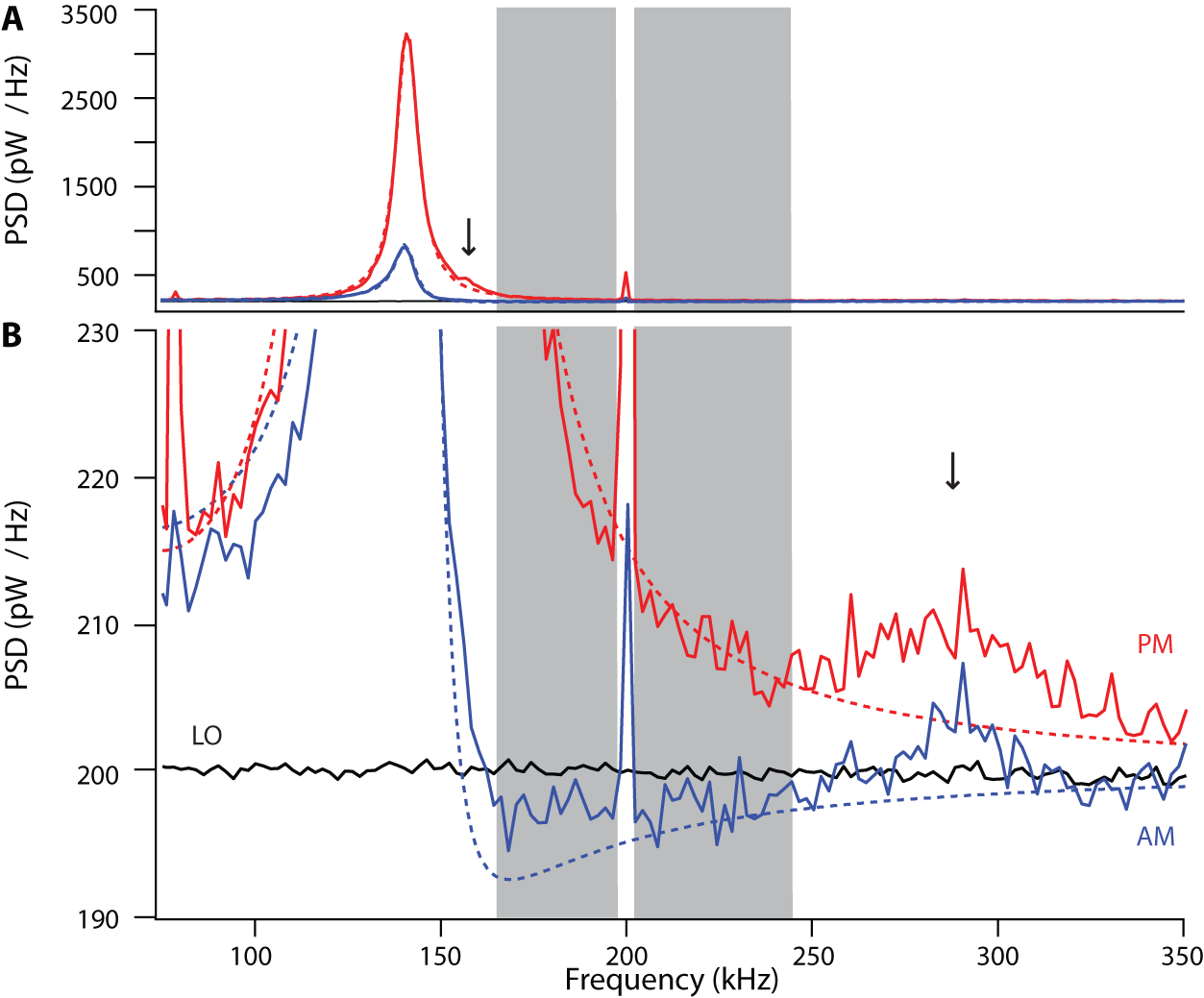
Ponderomotive squeezingThe collective motion of the atoms' center of mass can act to suppress quantum noise fluctuations of the probe light. This suppression is called ponderomotive squeezing. When the main source of noise on our probe light is photon shot noise, the optomechanical system is dominantly driven by these quantum fluctuations in radiation pressure. In such a system, by detuning our probe light from cavity resonance we close the gain loop and allow the optomechanical response to interfere constructively and destructively with input optical fluctuations, leading to spectral windows of amplification and of sub-shot-noise squeezing.
|
||||||||||||||||||||||||||
| Recent Changes (All) | Edit SideBar | Page last modified on February 02, 2016, at 09:51 PM | Edit Page | Page History |
| Powered by PmWiki | ||